2020. 7. 31. 06:58ㆍ고등교육과정
전기 회로는 전지의 -와 +에 전선이 연결되어야만합니다. 그게 전기 회로입니다.
건전지

중간에 선을 기점으로 왼쪽은 자유전자들이 저장되어있고, 오른쪽은 전선을 타고 여행을 마치고 돌아온 전자들이 쉬는 공간입니다. 만약 왼쪽에서 자유전자들을 다 써버리면, 그것이 바로 건전지가 다 닳은것입니다.

전류는 전자들의 흐름을 말합니다. 즉 '움직임'을 얘기하는 것이죠. 그렇다면 어디로 흐를까요? 그 전에 전자들이 어디로 흐르는지 알아야합니다. 전자들은 -에서 +로 움직입니다. 바로 전기력때문인데요,
전자들은 - 전하이며, 건전지의 - 극에서 서로 밀어내는 척력이 생깁니다. 그래서, 움직이는 겁니다. 그리고, 건전지의 +극에서는 -극에서 보낸 전자들을 당기는 인력이 발생합니다. 전류의 단위는 A를 사용합니다.
1A = 1초동안 한면에 전자들이 6.25*10^18개가 지나감을 의미 합니다. 만약 10A라면 6.25*10^19개가 지나간 것이겠지요.

전류는 +에서 -로 흐릅니다. 전류는 전자들의 움직임을 얘기하는 것인데 왜 전자들의 방향과 다르냐, 하면 그저 별거 없습니다. 처음에 전류를 먼저 발견했고, 그 후에 전자라는 개념이 완성되었기 때문입니다. 아직까지도 이것을 바로 안바꾸는 이유는, 사실 +에서 -로 흐르나, -에서 +로 흐르나 연구하는데에는 상관이 없기 때문입니다.
어쨌거나 핵심은 자유전자들이 움직이는 까닭은 전기력 때문입니다.
전압
전압은 V 단위를 사용합니다.
일단 전압은 정말 압력이 아닙니다. 전자들을 움직이게 하는 능력이죠. 그게 뭐였죠? 바로 건전지의 -극과 +극이 자유전자들을 밀어내고 당겨 움직이는 바로 그것입니다. 즉, 이 건전지가 있는 회로에 내가 전자 한개를 두면, 건전지의 전압에 따라 움직입니다. 다시 한번 말하지만 전압은 정말 수압도, 기압도 아닙니다. 압력이라 하면 입자들이 일정 부피에서 꽉 차거나 아니면 그 양을 얘기하는것인데, 전기 도선은 항상 전자로 꽉차있습니다. 이 말은, 이 건전지가 항상 자신이 낼 수 있거나, 이 회로에 필요한 량만 정확히 보낸다는 말입니다.
저항
저항은 Ω 단위를 사용합니다.
저항은 전류의 흐름을 방해합니다. 아니, 전압을 방해합니다. 즉, 속도를 방해합니다.
누가 방해하냐 한다면, 자유전자가 아니라 움직이지 않는 원자(원자핵,전자)가 방해합니다. 전기력으로 방해하는데요, 빠르게 지나가는 자유전자들을 자신과 그것의 전기력(인력, 척력)으로 잠시 어떻게든 주춤하게 합니다. 이것이 부딪혔음을 말합니다. 실제로는 자유전자가 물리적으로 원자핵등에 충돌하지는 않습니다. 어쨌거나 1초동안 전선의 한 지점(단면)을 지나간 전자들의 갯수는 조금 줄어듭니다. 서로간 비례합니다.
저항은 어디에나 있습니다. 전선에도 있고, 뭐든간에 있긴 합니다. 같은 전압(빠르기..정도가 되겠습니다)을 주었는데, 어떤 것은 1초동안 6.25*10^30개의 전자가 지나가고, 어떤것은 6.25*10^10개의 전자가 지나간다면, 어느것이 저항을 크게 받았을까요? 맞습니다. 6.25*10^10입니다. 저항을 많이 받았으니 1초동안 지나가는 전자의 갯수도 적겠죠.(속도가 느려졌습니다)
도선의 길이에 따라 저항의 크기는 비례합니다. 2배가 된다면, 저항도 2배가 됩니다. 전선 1cm당 저항 1옴이라면 3cm라면 3옴. 이렇습니다.
도선의 굵기에 따라 저항의 크기는 반비례합니다. 왜 일까요? 반지름 1이고 길이가 1인 전선이 저항 1옴이라면 반지름이 2로 늘어나면 마찬가지로 저항의 원인인 원자들이 늘어나서 저항이 커지는것 아닌가요? 아닙니다.

파란게 전자고 빨간게 원자입니다. 저것을 보시면 원자 사이를 자유전자가 통과하고있습니다.(실제로는 너무 작아서 서로 거리가 아주 멉니다). 그럼 똑같이 원자의 갯수도 2배로 증가되고 단면적도 2배로 증가된것을 볼까요?

저항의 양도 늘어났지만, 전자들도 마찬가지로 2배 넘게 들어갈 수 있어서 결과적으로는 저항이 낮아지는 셈입니다.
옴의 법칙
옴의 법칙 수식은 L = V/R입니다. L은 전류, V는 전압, R는 저항입니다.
8볼트, 총 저항이 4옴인 직렬회로(저항 = 모든 저항 합)에서 1초동안 지나는 전자의 갯수는 2A입니다.
저항이 4옴, 전류가 2A라면 전압은 8볼트여야만 합니다.
전류가 2A, 전압이 8볼트라면 전체 저항은 4옴이 되겠습니다.
직렬연결
직렬연결은 하나의 선으로 시작해서 하나의 선으로 끝납니다. 갈래길이 없습니다.

조금전 모든것에 앵간하면 저항이 있다했는데 전구도 마찬가지입니다. 저 전구가 만약 3옴의 저항을 가지고 있다 합시다. 건전지는 9V고, 그럼 전류는 3A입니다. 여기서 전체 저항은 3옴입니다. 그런데 만약 전구를 한개더 추가하면 저항의 길이가 길어지는 셈입니다. 그래서 저항도 커집니다.

위 상태에서 왼쪽 전구는 켜질까요? 척력으로 인해서 전자가 밀려나지는 않을까요? 켜지지 않습니다. 왜 안켜지냐면, 전구가 켜지는 이유는 그 전기의 흐름, 전류 때문입니다. 전자 때문이 아니라, 수많은 전자가 흐르면서, 지나가기 때문입니다. 위 처럼 +가 끊겨서 자유전자들이 제대로된 방향을 잡지 못합니다. 우왕자왕하는 것이죠.
만약 전선에 전자가 꽉 찬다면, 그것은 그저 멈춥니다. 건전지는 자신이 내야만할 최소한의 전자만 보내기 때문이죠.
직렬연결은 전류의 양이 같습니다. 두갈래길로 나뉘지 않고 한개의 전선에서 쭉 가기 때문이죠. 하지만 가다가 저항에 의해 전류의 세기가(1초에 몇개의 전자가 지나느냐) 약해집니다. 그러다가 또 약해집니다. 결국에 직렬의 전류 세기라 하면 모든 저항에서 깎이고 깎인 것들의 합이 되겠습니다.
병렬연결
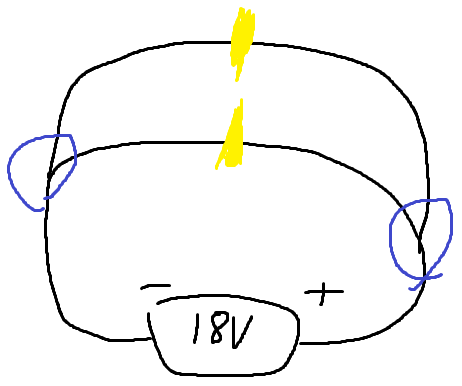
병렬연결은 갈림길이 있습니다.
저렇게 갈림길이 보이시죠?
왼쪽의 갈림길에서 전류가 반토막 납니다. 두 갈래길 때문이죠. 그럼 어떻게 두 갈래로 나뉘냐? 질문이 생기는데요, 이 전위차 때문에 그렇습니다. 기본적으로 처음 연결한다면 이제 막 전자들이 움직이기 시작하는데 그쯤에서 전자들이 갈림길을 마주한다면, 그 중에서 아주 미세하게, 아주아주 미세하게 약한곳으로 끌려갑니다. 그렇게 전자가 끌려가면 다음 전자는 반대껄 선택하게됩니다. 왜냐면 아까 그 첫번째가 들어감으로써 반전되었기 때문입니다.
어쨌거나, 저기서 (예시로) 6A에서 가다가, 갈림길에서 3A, 3A로 쪼개집니다.
그리고 그 각각의 전구들이 6옴의 저항을 가진다면, 전류 * 저항 = 전압, 이렇게 만족이 되며, 다시 오른쪽의 갈림길에서 3A, 3A이렇게 해서 만나 6A가 됩니다.
특징이 있습니다. 병렬연결에서 전류는 모든 전류의 합입니다.
무슨 말이냐 하면 마지막 갈림길에서 만난 전류들의 합이라는 것입니다. 그리고 하나더, '갈림길에서 전류가 반토막이 났는데 왜 전압은 같다고 하죠?'라고 물을 수 있는데, 전압은 속도라고 생각하십시오. 아니 그보다 더 보내는 힘을 생각하시면 되겠습니다. 기압같이 안의 기체 양이 반이 날아가면 기압이 낮아지는 것이 아닙니다.
건전지가 보내는 힘은 같습니다.
병렬연결에서의 저항 굵기에 따른 저항 감소
이게 무엇이냐면

위 그림입니다. 일단 a가 전류의 세기라 하겠습니다. 그렇다면 각각 a/2, a/2가 되겠죠? 그렇다면 옴의 법칙을 이용하여 각각의 저항을 구하겠습니다.
l1, l2는 왼쪽 갈림길에서 나누어진 전류입니다.
l1 = a/2, l2 = a/2, l1 + l2 = a
l1 * 3 + l2 * 3 = 6(v)입니다.
두 갈래로 나뉘어져 저항을 받은 것의 각각의 결과물 l1, l2 는 1이고, 1가 되었습니다. 그럼 이 전류를 다시 합쳐볼까요? 2입니다.
이번에는 직렬연결로 6옴의 저항을 설정하고 전류를 비교해보겠습니다.
a = 6/6이죠? 같은 전압을 흘리고 같은 저항의 총합을 보냈으나, 병렬연결에서는 2갈래길로 나눈다음에, 각각의 저항으로 통과시켰으니까 1초에 통과하는 전자수가 더 많아지는 것입니다! 즉, 이 말은 전압/저항=전류 인 부분에서, 전압은 고정이니 저항이 작아졌다는 말과 동일합니다.
쉽게 말해 저항 굵기가 굵어졌다는 말은 입구가 넓어져 오히려 저항이있음에도 불구하고 전자들이 더 많이 들어간다는 뜻입니다. 이렇게 보자면 이렇게 입구가 넓어진 부분에 대해서 비슷합니다. 그래서 이게 저항이 굵어진것과 같다고 하는것입니다.
감사합니다.
'고등교육과정' 카테고리의 다른 글
| 경사에서의 물체에 작용하는 중력을 두가지 벡터로 분해하기 (0) | 2020.11.06 |
|---|---|
| 피타고라스의 정리와 삼각함수, 2차원 평면에서의 사고 간편 암기 (0) | 2020.11.06 |
| 감각적인 표현으로 글을 쓰는 방법, 더 멋지게 글 쓰기! (0) | 2020.11.02 |
| <꽃 - 김춘수> 존재론에 대한 고찰 (0) | 2020.10.20 |
| 생물 - 꼼꼼히 여행하는 소화계 (0) | 2020.10.07 |