2020. 11. 6. 20:02ㆍ고등교육과정
1. 피타고라스의 정리
직각삼각형 ABC의 C가 직각일때 AC^2 + BC^2 = AB^2 입니다.
주의) 어떤 직각삼각형 ABC가 있을때, 그것을 변형시켜 다른 직각삼각형으로 만들었을 경우, 원래 직각이었던 부분은 바뀌어집니다. 그러나, 사용되는 기호는 같으니 착각하는 경우를 사전에 알아두세요.
2. 원그래프
X^2 + Y^2 = R^2 일때 R이 상수로써 작용한다면 R은 원 그래프의 반지름입니다.
3. 삼각함수 sin, cos, tan
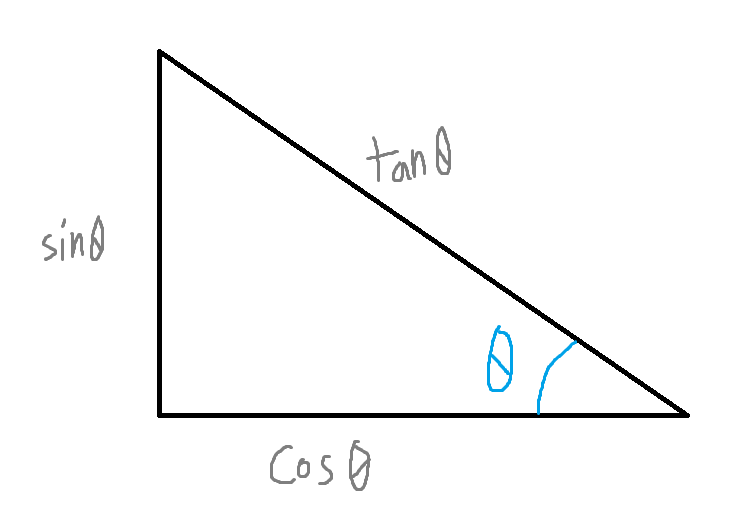
삼각함수를 이용해 좌표평면 원점을 중심으로 반지름이 1인 원을 그릴때 그 원에 위치하는 점들의 위치를 알 수 있습니다.
점을 제일 위 꼭짓점으로 잡고, 직각삼각형을 그립니다. 그리고 좌표평면의 원점에 근접한 각의 각을 구합니다. 가령 30도가 될 수 있습니다. 그렇다면, 그 점의 위치를 알 수 있습니다.
그 점의 위치는 (cos30도, sin30도) 입니다. 여기서 미루어 보아,삼각함수를 사용할땐 그 중심각을 잡고 사용하는 것을 볼 수 있습니다. (만약 다른 모양의 직각삼각형을 그려야한다면, 얻을 수 있는 값을 중심각으로 하는 직각삼각형을 그리되, 그에 따른 삼각함수를 주의해서 써야합니다.)
일반적인 직각삼각형에서 sin은 높이, cos은 밑변, tan은 빗변이라고 생각하시면됩니다.
직각삼각형 ABC에서, sin은 AC/AB, cos은 BC/AB, 그리고 tan은 BC/AC입니다.
4. 외워야할 값 - 특수각
삼각함수 값들은 유도할 수 있지만 가끔 유도못할때도 있습니다. 그런 경우에는 특수각이라고 하는 자주쓰는 삼각함수 값들을 쓰라는 의미입니다. 이것들은 양이 적으니 금방 외울수 있습니다.
특수각에는 30, 45, 60도가 있습니다. 0도와 90도는 sin을 y, cos을 x라고 보았을때 원이라고 생각하면 금방 알 수 있습니다. (0,1), (1,0)입니다.
1. sin
sin30도 = 1/2
sin45도 = 루트(2)/2
sin60도 = 루트(3)/2
2. cos
cos30도 = 루트(3)/2
cos45도 = 루트(2)/2
cos60도 = 1/2
서로 거꾸로인 것을 눈치채셨을 겁니다. 원이기 때문이죠.
감사합니다.
'고등교육과정' 카테고리의 다른 글
| 글의 작성, 하나의 무기로 만들기 (0) | 2020.11.28 |
|---|---|
| 경사에서의 물체에 작용하는 중력을 두가지 벡터로 분해하기 (0) | 2020.11.06 |
| 감각적인 표현으로 글을 쓰는 방법, 더 멋지게 글 쓰기! (0) | 2020.11.02 |
| <꽃 - 김춘수> 존재론에 대한 고찰 (0) | 2020.10.20 |
| 생물 - 꼼꼼히 여행하는 소화계 (0) | 2020.10.07 |