재미있는 수학문제 1탄
2020. 12. 11. 19:23ㆍ중등교육과정
반응형
어느날 오후 2시에 1시간에 60km를 이동하는 순찰 쾌속정이 반경 30km내의 모든 배들을 감지할 수 있는 레이더를 탑재하고 무인도 A에서 서쪽으로 150km 떨어진 곳을 지나는데 어떤 배 한척을 감지했다. 곧바로 그 배를 쫓기 위해 무인도 A와 나란한 선상에서 동쪽으로 이동을 시작했다.
그 이후 쾌속정이 그 배를 발견했을때 그 배는 무인도 A의 북쪽 20km에서 발견되었다.
(1) 쾌속정이 그 배를 발견했을때는 몇시였을까?
나는 항상 문제를 적당히 2차원 좌표평면으로 환경을 설정하고 머릿속에 그린다. 이 방법을 이용하여 문제를 풀어보자. 머릿속에 섬과 쾌속정, 배를 그린다. 그 후, 모두 익숙한 연한 회색의 격자 모선을 그린다. 완벽하다.
방금 당신은 머릿속에서 바다와 섬과 배 2척이나 그렸다.
이제 풀이를 시작하자.
어떻게 풀까?
간단하게 미지수가 1개 있는 일차방정식과 피타고라스의 정리를 사용하면 된다.
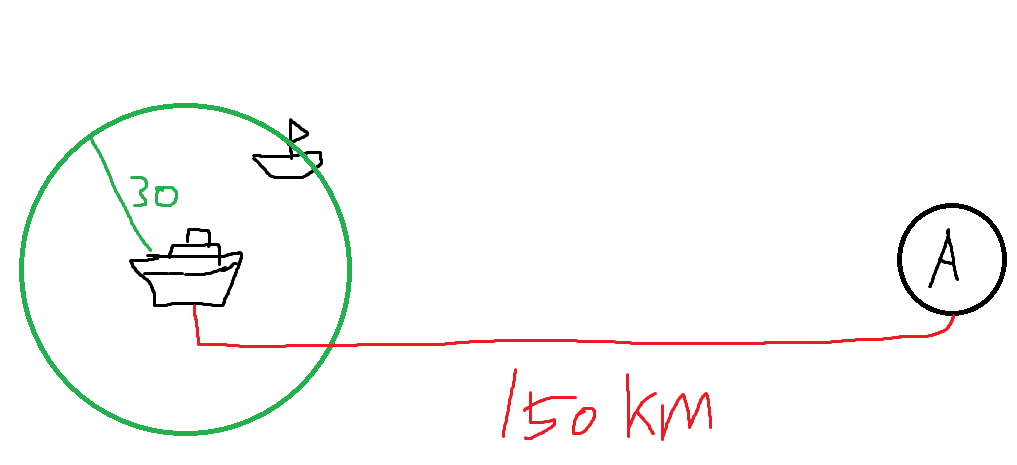
저 돗단배의 위치는 오비탈 내 전자위치 만큼 굳이 필요하지 않다. 어디있던간에 감지되었고, 30km안에 있다는. 아니 이것 조차 필요없다. 감지되었다는 것이 중요한 것이다. 그리고 시간이 오후 2시라는 것.

얼핏보면 삼각함수가 생각날 수 있는 문제다. 하지만 그러지 않아도 된다. 왜냐하면 우리의 목표는 발견했을때 시간이지 저 배의 위치가 아니기 때문이다.
쾌속정은 60km/h로 움직이기 때문에 오후 2시 + x/60가 정답이다.
그렇다면 x는 어떻게 구할 수 있을까? 새로운 정보인 돛단배의 위치를 이용하여서 풀 수 있다. 우리는 섬에서 150-x만큼 떨어져있고, 돛단배는 20km만큼 떨어져 있다. 서로 북쪽과 서쪽으로 섬과 수직을 이루고 있으며 이 말은 곧 피타고라스의 정리를 사용 할 수 있다는 것이다. 쾌속정과 돛단배의 직선거리, 즉 레이더가 감지 가능한 최대 거리는 30km임으로 우리의 직각삼각형 대각선의 길이는 30km이다.
(150-x)^2 + 400 = 900
이렇게 식을 세워 x의 값을 알아낼 수 있다.
끝
반응형
'중등교육과정' 카테고리의 다른 글
| [세계사] 로마제국의 부흥과 근본, 그리고 멸망 (0) | 2020.12.13 |
|---|---|
| [세계사] 안렉산드리아 제국의 정복기와 헬레니즘 (0) | 2020.12.13 |
| [세계사] 페르시아의 시작과 멸망과 또 다른 시작 (0) | 2020.12.13 |
| [세계사] 고대 그리스의 존재와 전쟁과 인물 (0) | 2020.12.13 |
| 조선의 국력의 쇠퇴 이야기와 백성들의 삶 (0) | 2020.12.13 |